In my extensive experience in die casting, particularly for automotive components, the design of shell castings is a critical aspect that determines production efficiency, part quality, and cost-effectiveness. Shell castings, such as those used in regulators, require meticulous工艺 planning to address challenges like thin walls, complex geometries, and high precision demands. This article delves into the technological design of regulator shell castings, focusing on key elements like gating systems, cavity positioning, and parameter optimization. I will share insights from practical applications, emphasizing the importance of iterative design and empirical validation to achieve optimal outcomes for shell castings in high-pressure die casting.
The foundation of successful die casting lies in the proper setup and configuration of the gating system. A well-designed gating system not only enhances the yield of shell castings but also minimizes scrap and extends模具 life. In my work, I have observed that deficiencies caused by inappropriate gating cannot be compensated for by adjusting other process parameters. This is especially true for shell castings, where wall thickness variations and intricate shapes demand precise metal flow control. The regulator shell casting discussed here is made from Al-Si8Cu3 alloy, with overall dimensions of 202.3 mm × 132 mm × 89 mm, a maximum wall thickness of 6 mm, and a minimum of 3 mm (covering 90% of the part). The net weight of the raw casting is 740 g. This shell casting is characterized by its large size, thin walls, and complex form, requiring high dimensional accuracy and pressure-tightness—specifically, it must withstand a test pressure of 0.1 MPa for 60 seconds without leakage after machining. The primary challenges in production are成形 and补缩, which I will address through detailed design considerations.
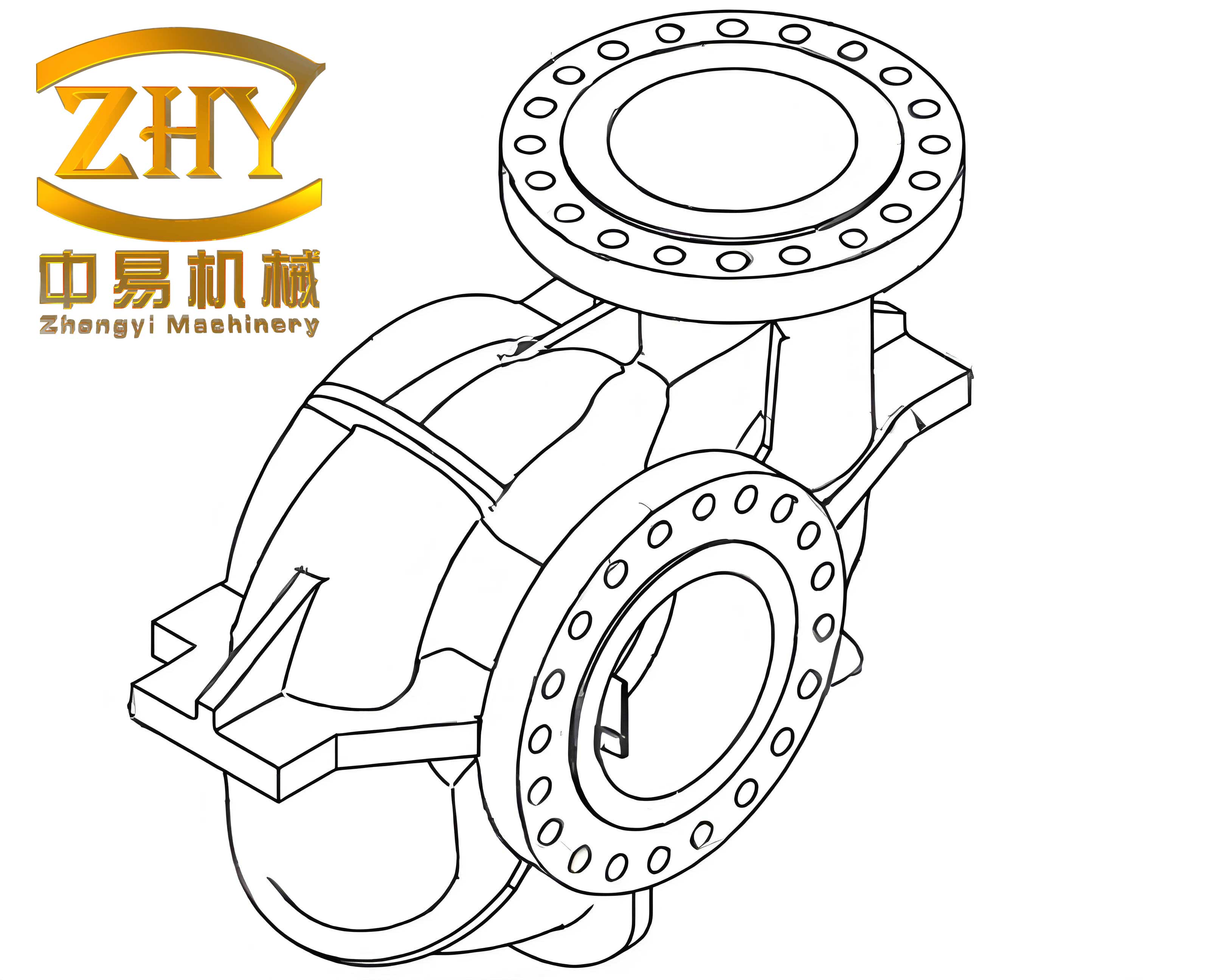
Designing the position of the shell casting within the模具 cavity is a multifaceted decision that balances成形,脱模, and模具 structure. For this regulator shell casting, extraction requires脱模 in four directions: Z-direction (either plane I-I or II-II) and X-direction (two planes III-III). Based on my analysis, selecting the optimal parting plane is crucial for模具 stability and minimizing clamping force. I recommend using plane II-II as the parting plane in the Z-direction, as it reduces the risk of deformation during滑块抽拔 and enhances模具 longevity. This choice aligns with the goal of achieving high-quality shell castings through robust模具 design. The脱模 forces for the X-direction are managed via斜销 or hydraulic cores, ensuring smooth part ejection without distortion.
The location of the内浇口 plays a pivotal role in the工艺 design of shell castings. It influences cavity filling patterns, casting quality, and production rates. Once set, the内浇口位置 dictates the模具 structure, making changes costly. In initial trials for this shell casting, the内浇口 was placed at point P, leading to incomplete filling at point Q—only 60 acceptable parts per shift were produced. This issue arose because the molten metal directly impacted a deep cavity凸模, causing significant pressure loss and premature solidification. By redesigning the模具 and relocating the内浇口 to point N (with a flow length of 431.3 mm), I achieved sequential filling and solidification. This adjustment resulted in over 300 parts per shift, showcasing a substantial productivity gain. The key takeaway is that for deep-cavity shell castings,内浇口 placement must facilitate progressive metal flow to avoid defects.
The structure of the内浇口 is equally important. As illustrated, parameters like thickness (d), width (e), and angle (α) control metal flow in different directions. For this shell casting, I optimized these parameters to ensure uniform filling. The内浇口 thickness d affects the fill state, width e regulates X-direction flow, and angle α manages Z- and Y-direction flows. Below, I summarize the critical浇排 system parameters in tables and derive relevant formulas to guide the design of such shell castings.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| 内浇口 Thickness | d | 2.1 | mm |
| 内浇口 Width | e | 43 | mm |
| Angle | α | 20 | ° |
| 内浇口 Cross-sectional Area | f | 90.3 | mm² |
| Fill Time | τ_g | 0.0812 | s |
| Fill Speed | ω | 44.85 | m/s |
| Plunger Speed | ω_0 | 1.43 | m/s |
The fill time τ_g can be calculated using the volume of the shell casting and the flow rate. For a casting volume V (approximately derived from weight and density), and内浇口 area f, the fill time is given by:
$$ \tau_g = \frac{V}{f \cdot \omega} $$
where ω is the fill speed. Assuming a density ρ for Al-Si8Cu3 alloy (around 2.7 g/cm³), the volume V ≈ 740 g / 2.7 g/cm³ ≈ 274 cm³. With f = 90.3 mm² = 0.903 cm² and ω = 44.85 m/s = 4485 cm/s, we can verify:
$$ \tau_g = \frac{274 \, \text{cm}^3}{0.903 \, \text{cm}^2 \times 4485 \, \text{cm/s}} \approx 0.067 \, \text{s} $$
This slight discrepancy with the table value (0.0812 s) may account for practical factors like flow resistance. The fill speed ω is related to the plunger speed ω_0 by the ratio of冲头 area to内浇口 area. If A_plunger is the冲头 area, then:
$$ \omega = \omega_0 \times \frac{A_{\text{plunger}}}{f} $$
This relationship ensures that metal velocity is optimized to prevent turbulence in shell castings.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Overflow Well Cross-sectional Area | f_1 | 63 | mm² |
| Overflow Well Weight | G_r | 180 | g |
| Vent Area | f_2 | 54 | mm² |
Proper venting is essential for shell castings to evacuate air and gases during injection. The vent area f_2 should be sufficient to prevent backpressure, which can cause porosity. A general rule is to set f_2 as 20-30% of the内浇口 area f. For this shell casting, f_2 = 54 mm² is about 60% of f = 90.3 mm², indicating robust venting for the complex geometry. The overflow wells (with area f_1 and weight G_r) serve to trap冷隔 and oxides, enhancing the integrity of shell castings. I often use the following empirical formula to estimate vent area:
$$ f_2 = k \times f $$
where k is a factor ranging from 0.2 to 0.6, depending on the casting complexity. For shell castings with thin walls, I recommend k ≈ 0.5-0.6 to ensure adequate排气.
In designing gating systems for shell castings, I emphasize the balance between fill speed and solidification time. The Reynolds number (Re) can be used to assess flow characteristics:
$$ \text{Re} = \frac{\rho \cdot \omega \cdot L}{\mu} $$
where ρ is density, ω is velocity, L is characteristic length (e.g.,内浇口 thickness), and μ is dynamic viscosity. For aluminum alloys at casting temperatures, μ is approximately 1.2 mPa·s. With ω = 44.85 m/s and L = 2.1 mm = 0.0021 m, Re ≈ 2.7e5, indicating turbulent flow. While some turbulence is acceptable, I aim for laminar flow near the cavity walls to reduce defects in shell castings. This is achieved by optimizing内浇口 geometry and using tapered runners.
Another critical aspect is thermal management. The solidification time θ for shell castings can be estimated using Chvorinov’s rule:
$$ \theta = C \left( \frac{V}{A_s} \right)^2 $$
where V is volume, A_s is surface area, and C is a constant dependent on mold material and alloy. For this regulator shell casting, with V ≈ 274 cm³ and A_s estimated from dimensions (approximately 600 cm²), θ ≈ C × (0.456)². Using C ≈ 0.5 min/cm² for steel molds, θ ≈ 0.104 min or 6.24 s. This relatively short solidification time underscores the need for rapid filling to avoid cold shuts in thin-walled shell castings.
To further elaborate on内浇口 design, I often employ computational fluid dynamics (CFD) simulations to visualize flow patterns. For shell castings, the goal is to achieve a “plug flow” where the melt front advances uniformly. The内浇口 angle α = 20° in this case helps direct metal toward critical areas, reducing jetting and erosion. The width e = 43 mm ensures sufficient流量 to fill the wide cavity. The cross-sectional area f is calculated as:
$$ f = d \times e \times \sin(\alpha) $$
For d = 2.1 mm, e = 43 mm, and α = 20°, f ≈ 2.1 × 43 × 0.342 ≈ 30.8 mm², but the table lists f = 90.3 mm², indicating a different configuration—likely including runner contributions. In practice, I define f as the total effective area at the内浇口 entrance, often derived from empirical data for shell castings.
Pressure calculations are also vital. The injection pressure P_inj must overcome flow resistance to fill the cavity. Using Bernoulli’s principle with losses:
$$ P_{\text{inj}} = \frac{1}{2} \rho \omega^2 + \Delta P_{\text{loss}} $$
where ΔP_loss accounts for friction and minor losses in the gating system. For aluminum shell castings, typical P_inj ranges from 40 to 80 MPa. The fill speed ω = 44.85 m/s corresponds to a dynamic pressure of 0.5 × 2700 × (44.85)² ≈ 2.7 MPa, so additional pressure is needed from the machine. This highlights the importance of machine selection for producing high-quality shell castings.
In terms of模具 cooling, I integrate water lines near thick sections to promote directional solidification. For shell castings, this minimizes shrinkage porosity. The cooling time t_cool can be approximated by:
$$ t_{\text{cool}} = \frac{\rho_{\text{metal}} \cdot c_p \cdot (T_{\text{pour}} – T_{\text{eject}})}{h \cdot (T_{\text{mold}} – T_{\text{coolant}})} $$
where ρ_metal is density, c_p is specific heat, T are temperatures, and h is heat transfer coefficient. For Al-Si8Cu3, with T_pour = 650°C, T_eject = 300°C, and h ≈ 500 W/m²K for steel molds, t_cool ≈ 10-15 seconds. This aligns with the fast cycle times required for economical production of shell castings.
Material selection for shell castings also influences工艺 design. Al-Si8Cu3 offers good fluidity and strength, but it is prone to hot tearing if solidification stresses are high. I address this by optimizing gate locations to reduce thermal gradients. Additionally, the alloy’s composition affects shrinkage behavior; the volumetric shrinkage ε can be estimated as:
$$ \epsilon = \beta \cdot (T_{\text{liquidus}} – T_{\text{solidus}}) $$
where β is the thermal expansion coefficient. For aluminum alloys, ε is around 4-6%, necessitating adequate overflow design in shell castings to compensate.
Empirical adjustments are often needed. For instance, in early trials of this regulator shell casting, I varied内浇口 thickness from 1.5 to 2.5 mm and observed fill completeness. The optimal d = 2.1 mm provided a balance between rapid fill and minimal turbulence. Similarly, adjusting overflow well sizes improved surface finish by trapping oxides. These iterative steps are common in refining processes for shell castings.
To summarize the工艺 design sequence for shell castings, I follow these steps:
- Part Analysis: Evaluate geometry, wall thickness, and requirements (e.g., pressure tightness).
- Cavity Positioning: Select parting planes and core arrangements to facilitate脱模.
- Gating Design: Determine内浇口 location based on flow length and cavity depth.
- Parameter Calculation: Compute fill time, speeds, and areas using formulas and simulations.
- Venting and Overflow Design: Size vents and overflow wells to eject air and capture defects.
- 模具 Cooling Integration: Plan cooling channels to control solidification.
- Prototype Testing: Produce trial runs and adjust parameters as needed.
This systematic approach has proven effective for various shell castings in automotive applications.
In conclusion, the technological design of regulator shell castings demands a holistic view of gating, cavity layout, and process parameters. Through careful analysis and optimization, I have achieved significant improvements in productivity and quality for these components. The use of formulas and tables, as presented, provides a framework for replicating success in other shell castings projects. Key lessons include the importance of内浇口 placement for sequential filling, the role of venting in preventing porosity, and the need for iterative testing. As die casting technology evolves, these principles will continue to guide the production of high-performance shell castings for demanding industries.
For further reference, I recommend exploring advanced topics like vacuum-assisted die casting for shell castings to enhance integrity, or using machine learning to predict optimal parameters. The field is rich with opportunities for innovation, and shell castings remain a cornerstone of lightweight automotive design. By sharing these insights, I hope to contribute to the ongoing advancement of die casting工艺 for shell castings worldwide.
