1. Mathematical model of filling process
The metal liquid is poured through the pouring system for mold filling casting. In the simulation of the filling process, fluid mechanics is used as the basis, involving continuous equations, energy equations, etc.
The expression for a continuous equation is:
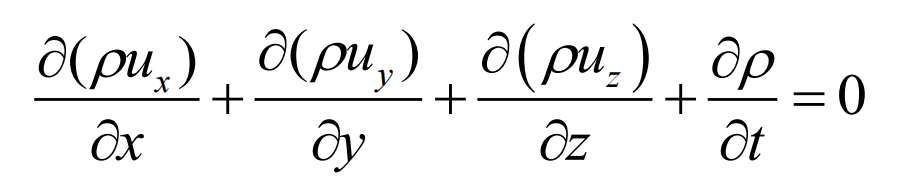
In the formula, ux, uy, and uz are the components of the velocity of the molten metal in the x, y, and z directions, respectively; T is time; ρ For liquid density.
For incompressible fluids, partial ρ/∂ T=0, the expression for the continuous equation is:
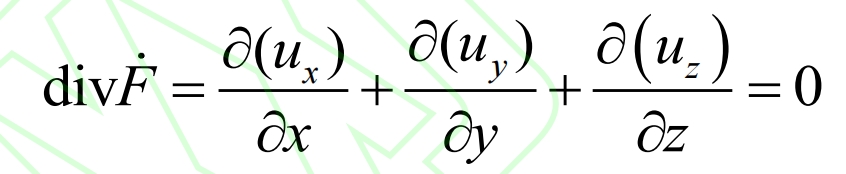
In the formula, div Ḟ is the divergence.
The mathematical expression for the energy equation is:
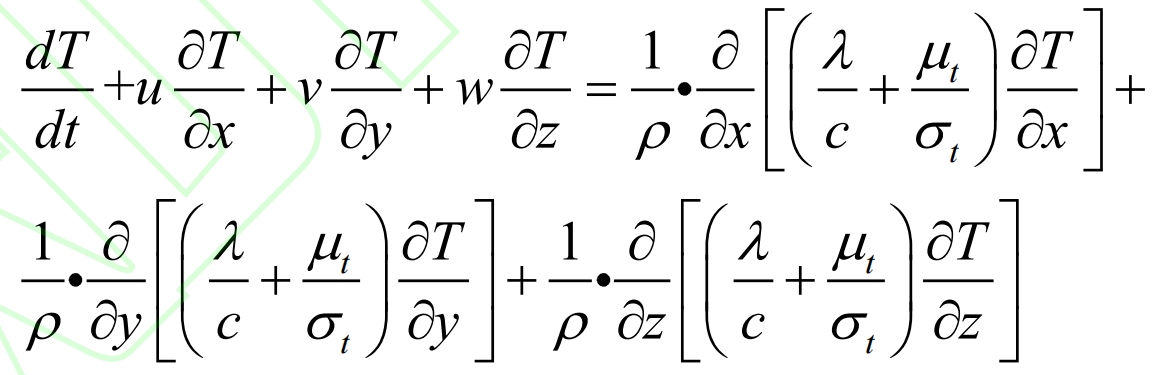
In the formula: λ Is the thermal conductivity coefficient in the fluid; T is the temperature of the fluid; μ T is the turbulent dynamic viscosity; σ T is the turbulent Prandtl number, generally σ T=0.9~1.0.
2. Mathematical model of solidification process
When the metal liquid is filled into the mold and begins to transition from liquid to solid, effective calculation of the solidification process can prevent and control the occurrence of casting defects. Based on thermodynamic laws, complete heat transfer forms such as heat conduction, convection, and radiation between the rocker arm shell casting and the mold, as well as between the air. The pouring system of the rocker arm shell of the coal mining machine this time is mainly based on heat conduction, ignoring the effects of heat transfer forms such as convection and radiation.
The conduction mode of metal liquid injected into the mold cavity in the sand box is mainly unstable heat conduction, and its control equation is:
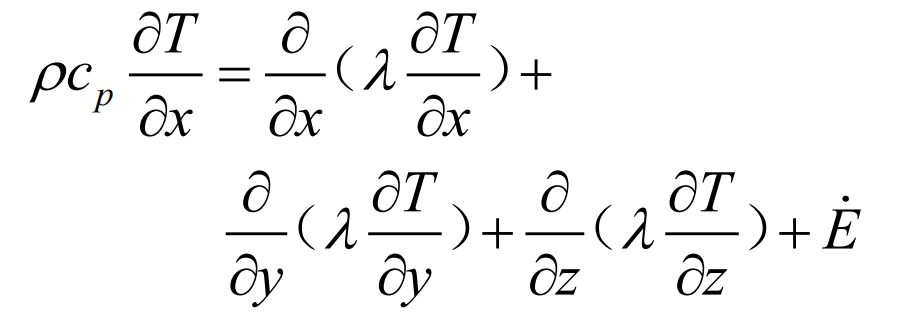
In the formula: cp is the specific heat capacity at constant pressure; λ Is the thermal conductivity; Ė The heating rate of a heat source in an object per unit time and volume.
3. Mechanism and prediction criteria for shrinkage and porosity formation
Due to the unreasonable design of the feeding mechanism, the casting of the rocker arm shell will experience local volume shrinkage during the solidification and cooling process, and the holes formed by shrinkage need to be promptly supplemented by molten metal [25-26]. The Niyama criterion is widely used for predicting shrinkage and porosity due to its accurate judgment, and its expression is:
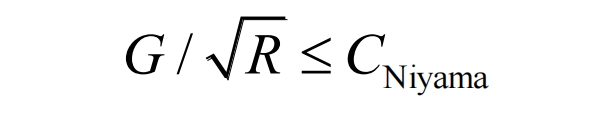
In the formula: G is the temperature gradient; R=(Tmi, j, k-Tm+1i, j, k)/∆ t is the cooling rate; CNiyama is the critical parameter value for determining whether shrinkage and porosity occur.
In the Niyama criterion:
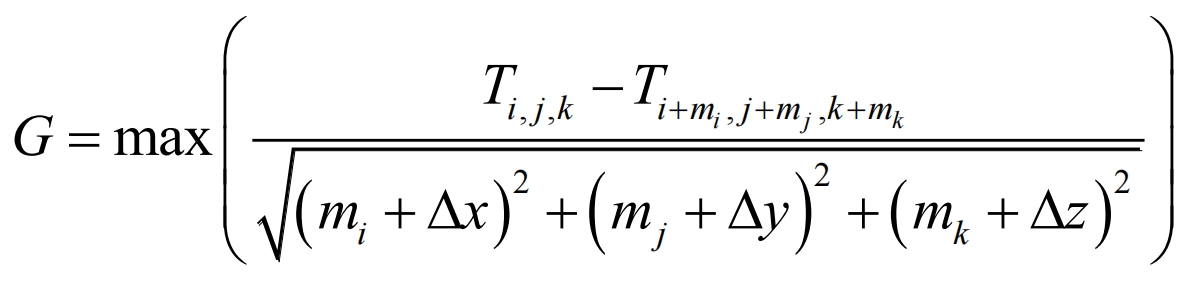
In the formula: mi, mj, and mk are the units of measurement (i, j, k) adjacent to unit m in the x, y, and z directions; ∆ x. ∆ y and ∆ z are unit step sizes.
4. Establishment of stress mathematical model
Using an equivalent stress calculation model to represent the stress distribution of the rocker arm shell casting, the mathematical expression is:
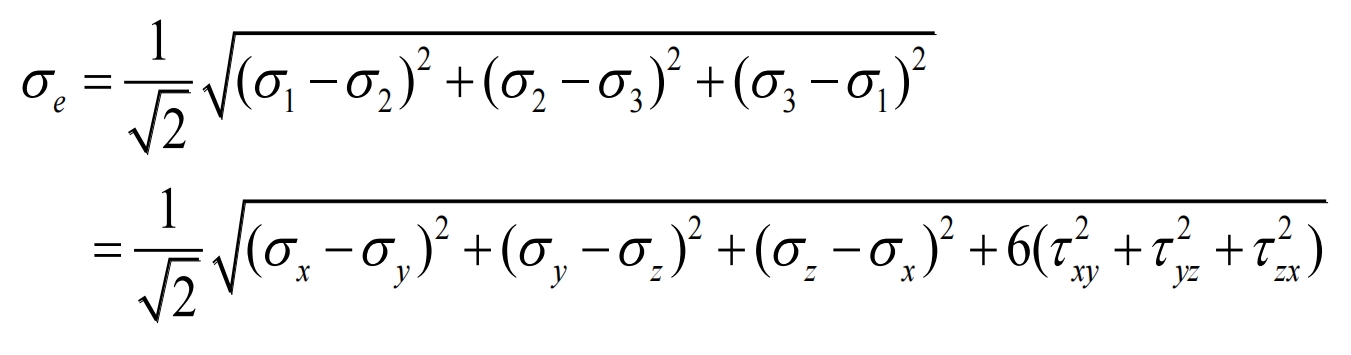
In the formula: σ 1 σ 2 σ 3 are the first principal stress, the second principal stress, and the third principal stress, respectively; τ Ij is the shear stress; σ E is the equivalent stress.
