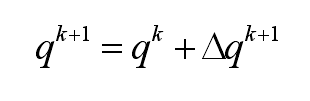In squeeze casting process, the solidification process involves phase transformation, and the thermophysical properties of related parameters are temperature dependent, so the inverse calculation of heat conduction is actually a nonlinear problem. In order to estimate the interface heat transfer coefficient with solidification time more effectively, the finite difference method based on Beck algorithm is used to discretize the equation.
The heat transfer inside the mold (from the mold surface to the farthest temperature measuring point) can be described by formula,
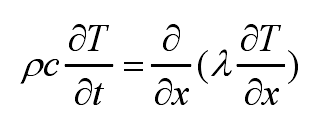
Where, ρ, C and λ are the density, specific heat and thermal conductivity of the mold, respectively. ρ, C and λ change with temperature.
The initial and boundary conditions are expressed by the following expressions:
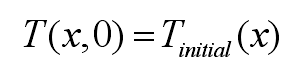
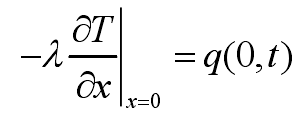
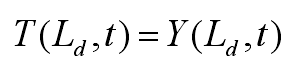
Where, tinitial is the initial temperature of the die, q is the heat flow of the casting die interface, LD is the distance from the farthest temperature measuring point to the die surface, and Y (LD, t) is the measured temperature at LD. The temperature measurement area (0 ≤ x ≤ LD) in the die can be divided into m equidistant grids (LD = m Δ x), and I subscript is x discrete node number. If the appropriate time interval Δ t is selected, the time domain can be discretized as t = k Δ t. The subscript k is used to mark different time steps. Subscript I is the number of discrete nodes. In order to solve the equation, implicit difference is used to discretize the equation. For the nodes on the die surface, the formula can be sorted into the following formula:
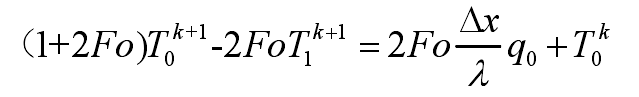
For the internal nodes of the mold, the formula can be sorted into the following formula:
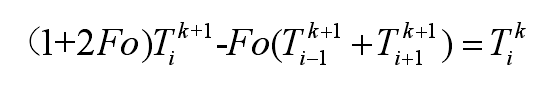
Where fo is Fourier number and its finite difference scheme is as follows:
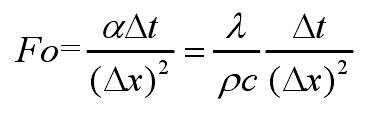
By solving the inverse heat conduction problem, the heat flux of the casting die interface can be obtained at each time step. The core of the anti algorithm based on Beck algorithm is realized by minimizing the following formula:
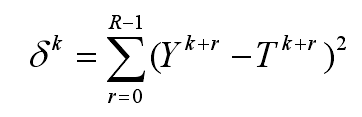
Through Taylor expansion, the solution of the formula can be transformed into the solution of the formula
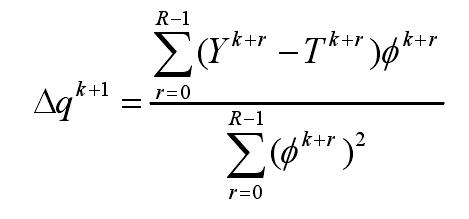
Where R is the total duration of the future time step, r = R Δ T, and φ is the sensitivity coefficient, and its definition is shown in the formula,
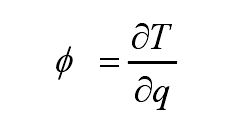
The heat flux QK + 1 in the next time step is corrected by adding QK and Δ QK + 1