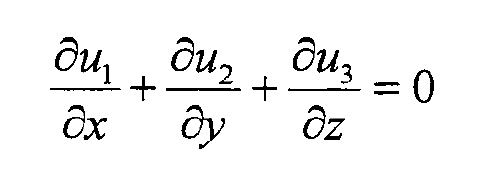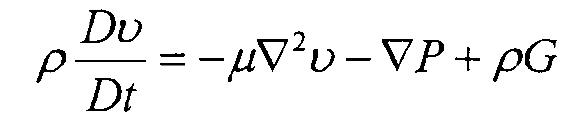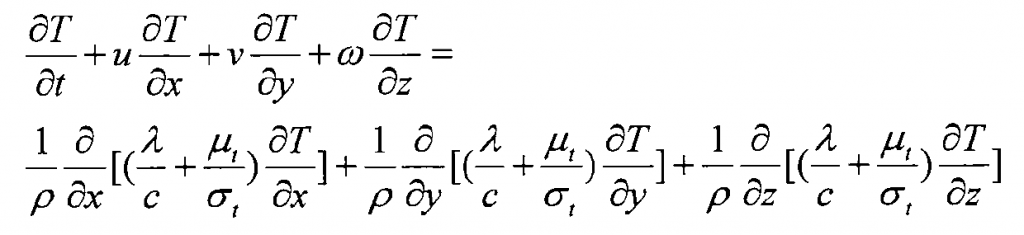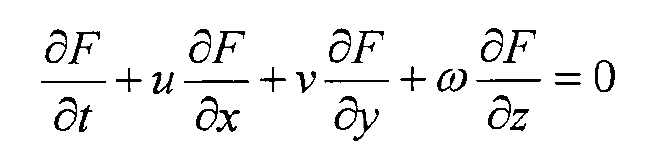The filling process of metal liquid in sand mold casting is a very complex heat exchange process, which is accompanied by heat loss and solidification, and the metal liquid in sand mold casting is in non constant temperature flow movement. The flow process follows the laws of mass conservation, momentum conservation and energy conservation. Therefore, continuity equation, momentum equation, volume function equation and energy equation group can be used to describe this process.
The law of mass conservation can be expressed as that the increase of mass in the control unit is equal to the mass flowing into the unit from the surrounding unit. Assuming that the fluid is incompressible, the mathematical expression is:
Where U1, U2, U3 and are the components of the velocity vector in three directions (x, y, z).
The momentum conservation equation, also known as Navier Stokes equation, or N-S equation for short, assumes that the fluid is incompressible. At this time, its mathematical expression is as follows:
Heat exchange is always accompanied by the filling and flow process of liquid metal in sand mold castings. The heat exchange between liquid metal and mold in sand mold castings will cause heat loss of liquid metal, continuous reduction of temperature, and even solidification, which will affect the filling process of liquid metal. Therefore, when studying the fluid flow in the liquid metal filling process, we must consider the heat transfer between the liquid metal and the mold and the cold iron of the sand mold casting, so as to ensure that the simulation results are close to the reality.
According to the Fourier heat conduction law and the principle of energy conservation, the energy conservation equation of fluid heat transfer can be deduced. After adding turbulence treatment, the mathematical expression of the energy conservation equation is:
Where: t is the temperature of the fluid and CP is the isobaric specific heat capacity of the fluid; λ Is the thermal conductivity of the fluid; μ T is turbulent dynamic viscosity; σ T is the Prandtl number, general σ T = 0.9-1.0.
For incompressible fluids, the volume function equation is:
Where, f is the volume function; u,v, ω Is the component of the velocity vector in the X, y and Z directions of the coordinate system.