1.Partial differential equation for heat conduction:
The solidification process of castings is a complicated phase transition process.Solidification is a dynamic process in which mass, heat and momentum are transferred.At the instant of filling, due to inertia, strong convection occurs in the liquid metal, and then the convection speed decreases rapidly. The solidification process of the casting can basically be considered as a unsteady heat conduction process. Therefore, the numerical simulation of the solidification process of the casting can be converted into a mathematical solution of an unsteady heat conduction process.
In the course of solidification heat conduction, the relationship between temperature, time and space can be described by Fourier partial differential equation for heat conduction, i.e.
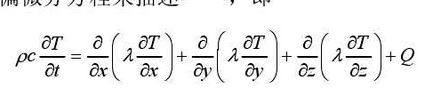
Where T is the temperature of the fluid, C is the specific heat capacity, lambda is the thermal conductivity of the fluid, and Q is the heat released per unit volume of time by an internal heat source, i.e. the latent heat of crystallization during the phase transition from liquid to solid during solidification.
2.Latent heat treatment:
The internal energy of the liquid phase of the same casting is larger than that of the solid phase, so the internal energy must be released when the alloy solidification changes from liquid phase to solid phase, which can be called latent heat of solidification (expressed in L).During solidification of castings, the latent heat released from solidification can be regarded as the lost heat. Therefore, the heat released from the latent heat is:
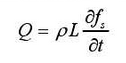
In the equation, L is the latent heat released when the unit mass metal reduces the unit temperature; FS is the solid phase ratio of the casting.
