As the conformal surface moves down under certain pressure and contacts with the rigid surface, the interface spacing decreases. Some bumps contact with the rigid surface to form a real contact area, and some do not contact with the rigid surface to form a non-contact area, as shown in Figure 1.
As shown in Figure 1, the contact area is the real contact area between the rigid surface and the integrated surface. Therefore, the heat transfer in the contact area is contact heat conduction. The thermal conductivity of the integrated surface is λ sum. Because the integrated surface is the equivalent contact surface of H13 steel, water-based graphite and A356 aluminum alloy, it is known from the discussion that the water-based graphite has a certain thickness and its thermal resistance is much larger than that of metal, so the thermal conductivity of the integrated surface is similar to that of the water-based graphite,
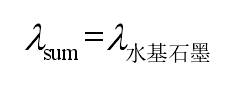
The contact thermal resistance of the real contact area is,
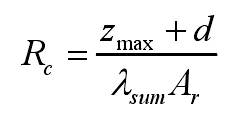
As shown in Figure 1, the non-contact area is composed of a gap filled with mixed gas and a metal part between the integrated surface and the rigid surface. The gas mixture consists of air and a small amount of water-based graphite. Because the gap is very small, the heat transfer of the gap is heat conduction. The thermal conductivity of the mixture is λ gas. For the non-contact region, the thermal resistance of the metal is very small compared with that of the gas mixture in the gap, so the gap thermal resistance can be used to represent the thermal resistance of the non-contact region. Yovanovich proposed the following thermal resistance model of non-contact region,
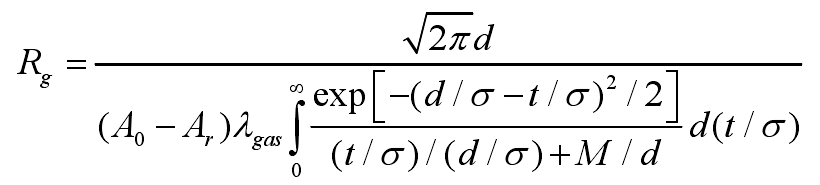
Where t is the length of the micro element heat flow channel or the thickness of the local gap, which is only related to the surface profile. σ is the roughness parameter related to the surface profile, and M is the thermal adaptation coefficient. Therefore, for a given interface, the gap thermal resistance is a function of the interface spacing,
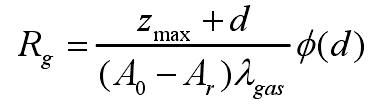
Where, φ (d) is a coefficient function only related to the interface spacing,
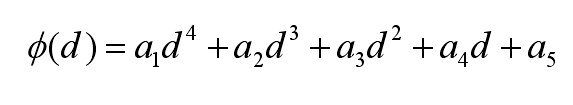
The interface heat transfer coefficient can be obtained by analyzing the interface thermal resistance,
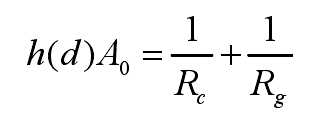
Because it is very difficult to obtain the coefficient function (d) by theoretical analysis, the data obtained from squeeze casting experiments are used to fit the coefficient function. The interface pressure and interface temperature obtained by squeeze casting experiment can get the corresponding interface spacing according to Fig. 2. The coefficient function can be fitted by using the interface heat transfer coefficient data and formula corresponding to the interface pressure and interface temperature obtained by experiment, and the parameters of the function can be obtained.
Based on the above micro geometry analysis, micro mechanics analysis and micro heat transfer analysis, the relationship between the interfacial heat transfer coefficient and the interfacial pressure and temperature can be established.


