1. Constitutive relationship of test cast steel under different dynamic loads
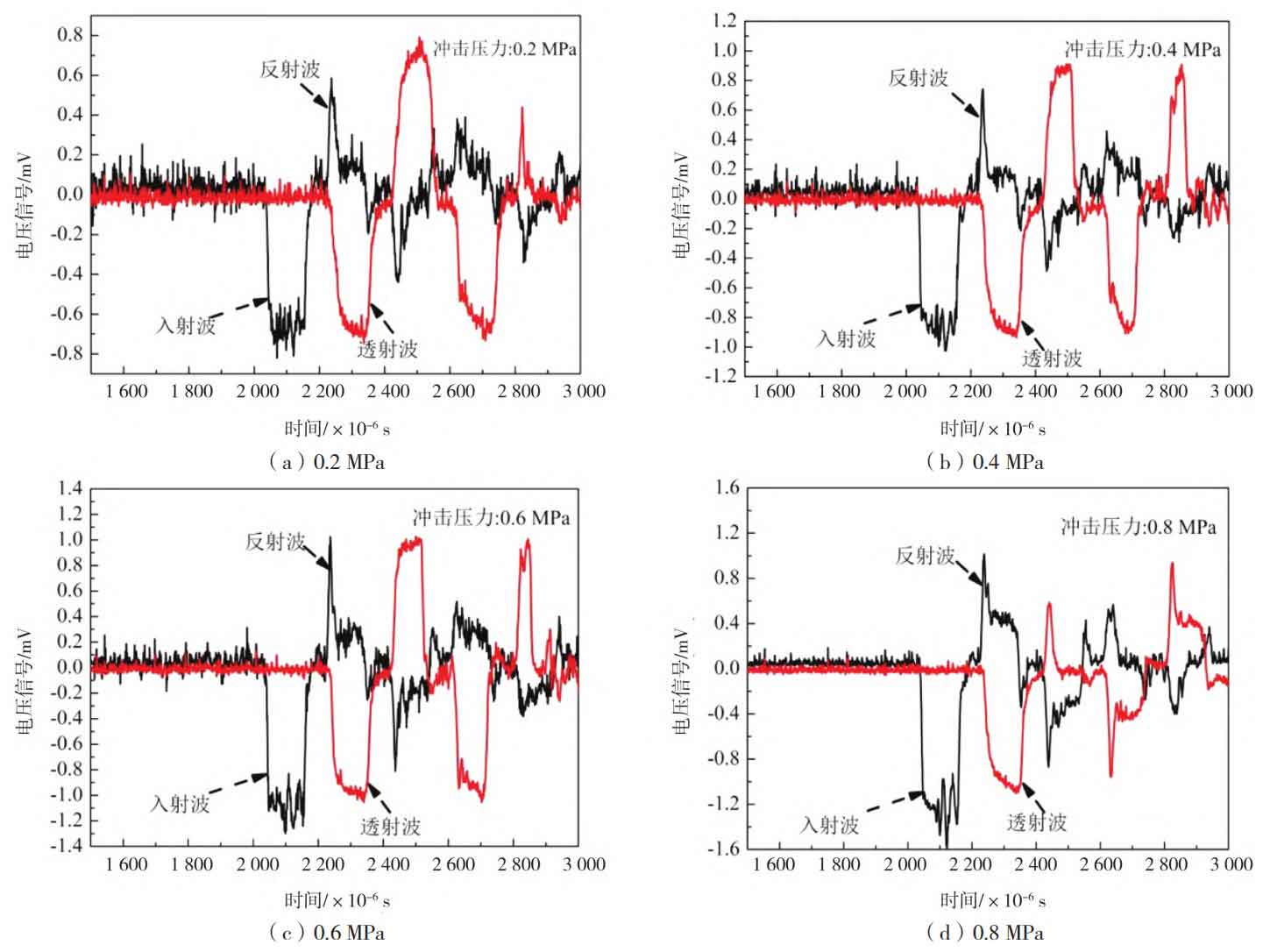
Based on the working principle of the SHPB device, it can be inferred that the stress-strain constitutive relationship of test cast steel under different dynamic loads can be obtained by collecting signals of incident waves, reflected waves, and transmitted waves caused by the impact load of the test material, as well as analyzing the strain changes measured by the resistance strain gauges of the incident and transmitted rods. Figure 1 shows the oscilloscope curves collected during the experiment under different dynamic loads. The strain caused by incident waves, reflected waves, and transmitted waves under different dynamic loads can be correlated using the following relationship:
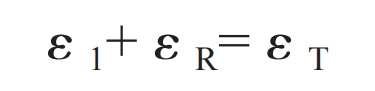
In the formula: ε 1 is the magnitude of alloy strain caused by the incident wave measured on the incident rod, ε R is the magnitude of alloy strain caused by transmitted waves measured on a transmission rod, ε T is the magnitude of strain caused by the residual wave signal after subtracting the transmitted wave from the incident wave.
Assuming that the interface velocity between the impact specimen and the incident rod is v1, the interface velocity between the impact specimen and the transmission rod is v2, and the partial derivatives of the interface displacement u1 and interface displacement u2 time t are taken, then the two interface velocities v1 and v2 can be defined by the formula:
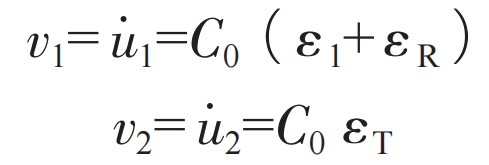
In the formula: where E is the Young’s modulus of the material, ρ The density of the material.
Based on the displacement of the two interfaces, the strain of the impact specimen can be further described by the formula:
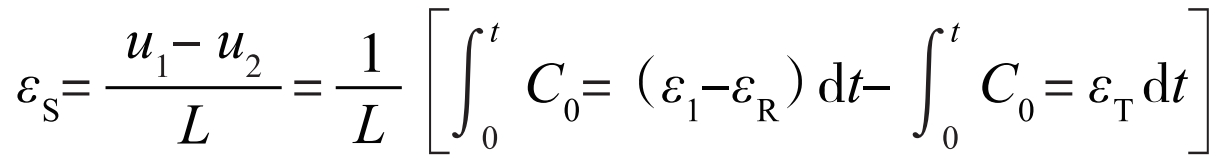
Further substituting the formula, simplifying and using strain to further calculate the partial derivative of time t, the expression for strain and strain rate of the sample is obtained as follows:
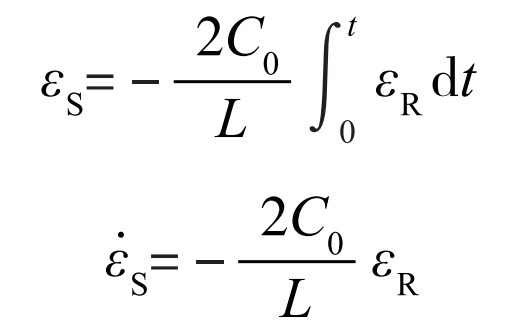
Due to the stress wave induced impact during the SHPB process, the two interfaces of the impact specimen should maintain a stress balance relationship. The sum of the stresses caused by the incident wave and reflected wave is the stress at the interface between the impact specimen and the incident rod, which can be described by a formula. Similarly, the interaction force between the impact specimen and the transmission rod interface can be obtained by calculating the stress caused by the transmission wave, and its expression is shown in the formula.
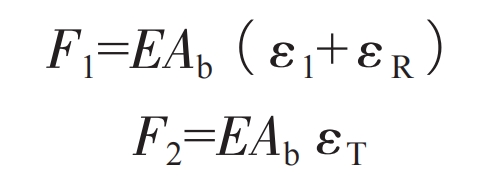
In the formula, Ab is the cross-sectional area of the incident rod and the transmitting rod.
Furthermore, the stress of the specimen is obtained by selecting the average value of the forces at the two interfaces, and the specific equation is as follows:
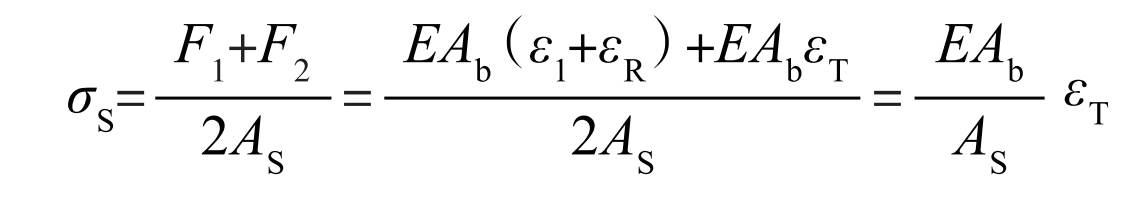
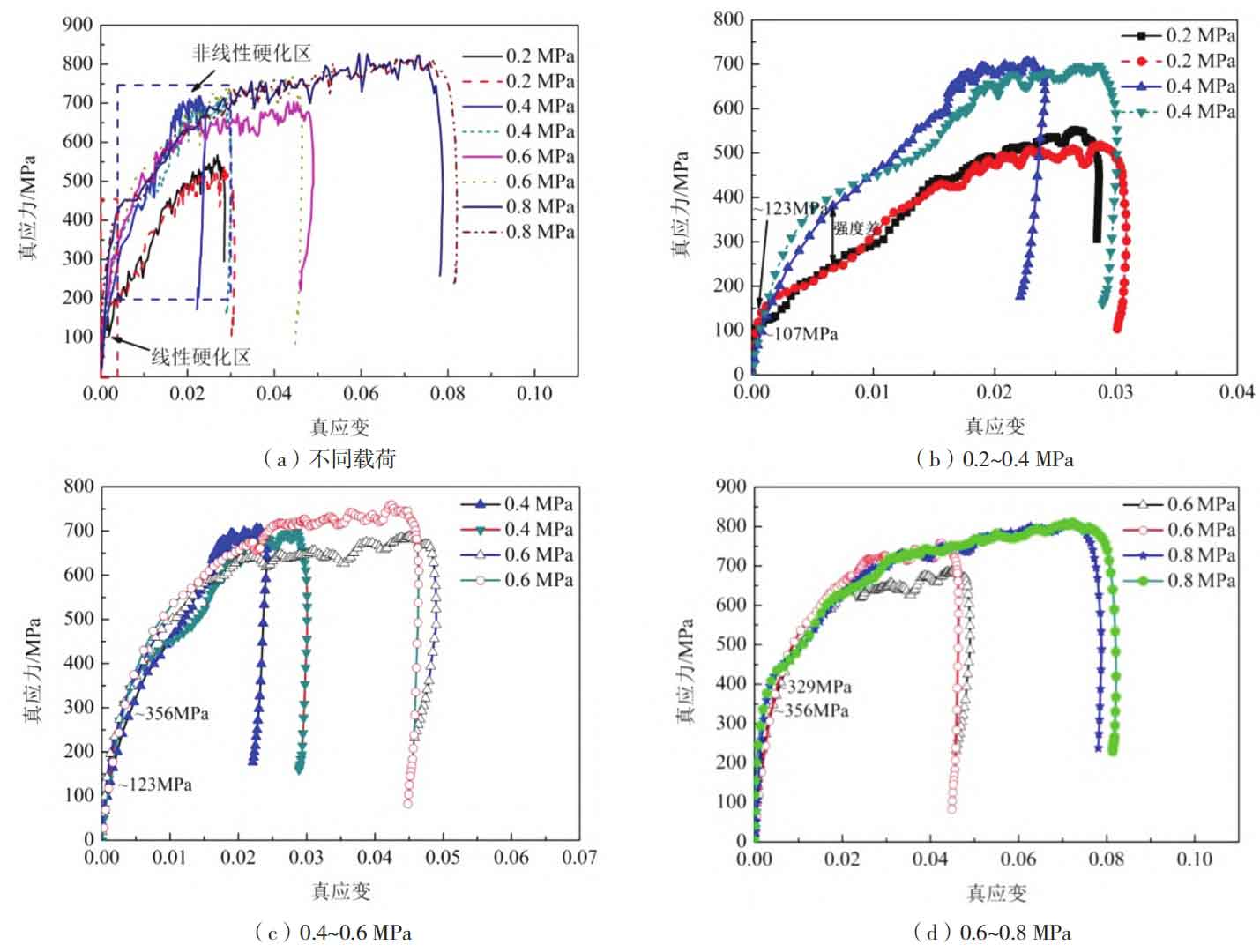
Based on the above theory and the results of the oscilloscope shock curve shown in Figure 1, the constitutive relationships of Mn13Cr2Mo under different shock loads are obtained as shown in Figure 2. From the figure, it can be seen that the constitutive relationship curves of Mn13Cr2Mo high manganese cast steel obtained under different impact loads exhibit some similar characteristics while also exhibiting certain differences. The similarity lies in the variation of the slope of the stress-strain curve with increasing strain. The stress-strain curve under different impact loads can be approximately decomposed into two parts: linear hardening zone and nonlinear hardening zone. The difference lies in the difference in the critical strength of the transition from linear hardening zone to nonlinear hardening zone of the test cast steel under different impact loads, as shown in Figure 2a. In order to further compare and study the influence of different cylinder pressures (different impact loads) on the constitutive relationship of test cast steel, a comparative study was conducted on the constitutive relationship curves of test materials under different cylinder pressures. The strength corresponding to the boundary area between the linear and nonlinear stages on the constitutive relationship curve is approximately determined as the critical strength. As shown in Figure 2b, under a pressure of 0.2 MPa, the stress increases linearly with the increase of strain. When the stress increases to about 107 MPa, the constitutive relationship curve undergoes a transition from a linear stage to a nonlinear stage; As the pressure increases to 0.4 MPa, the critical stress for the transition from linear hardening to nonlinear hardening in the constitutive relationship curve is about 123 MPa; When the pressure increases to 0.6 MPa and 0.8 MPa, the critical stresses for the transition from linear hardening to nonlinear hardening in the constitutive relationship curve reach about 356 MPa and 329 MPa, respectively, as shown in Figure 2b and c; From this, it can be seen that with the increase of experimental pressure, the critical stress of the transformation from linear hardening to nonlinear hardening stage in the deformation process of test cast steel under dynamic load significantly increases. Especially in the transformation process from 0.4 MPa to 0.6 MPa, the critical strength of the transformation increases from 123 MPa to 356 MPa, indicating that the increase of pressure can improve the critical stress of the initial linear hardening stage of Mn13Cr2Mo high manganese cast steel used in the experiment. At the same time, as deformation enters the nonlinear hardening zone, the strain hardening law under different impact loads is not the same. The strengthening effect of the nonlinear hardening zone at a pressure of 0.2 MPa is significantly lower than that under the condition of 0.4 MPa, as shown in Figure 2b. When the pressure is higher than 0.4 MPa, the strengthening law of the nonlinear hardening zone remains almost unchanged. The different slopes of stress changes during the nonlinear hardening stage indicate different hardening patterns of materials under different experimental conditions. The deformation hardening behavior of Mn13Cr2Mo high manganese cast steel is closely related to its wear service life. Only through reasonable material selection, can the hardening law of the material be well matched with the stress state carried by the material, in order to fully exert its strengthening and wear resistance effects. Therefore, it is crucial to clarify the strain hardening laws in both linear and nonlinear hardening stages for understanding and applying Mn13Cr2Mo high manganese cast steel.
2. Deformation hardening mechanism of Mn13Cr2Mo high manganese cast steel under different dynamic loads
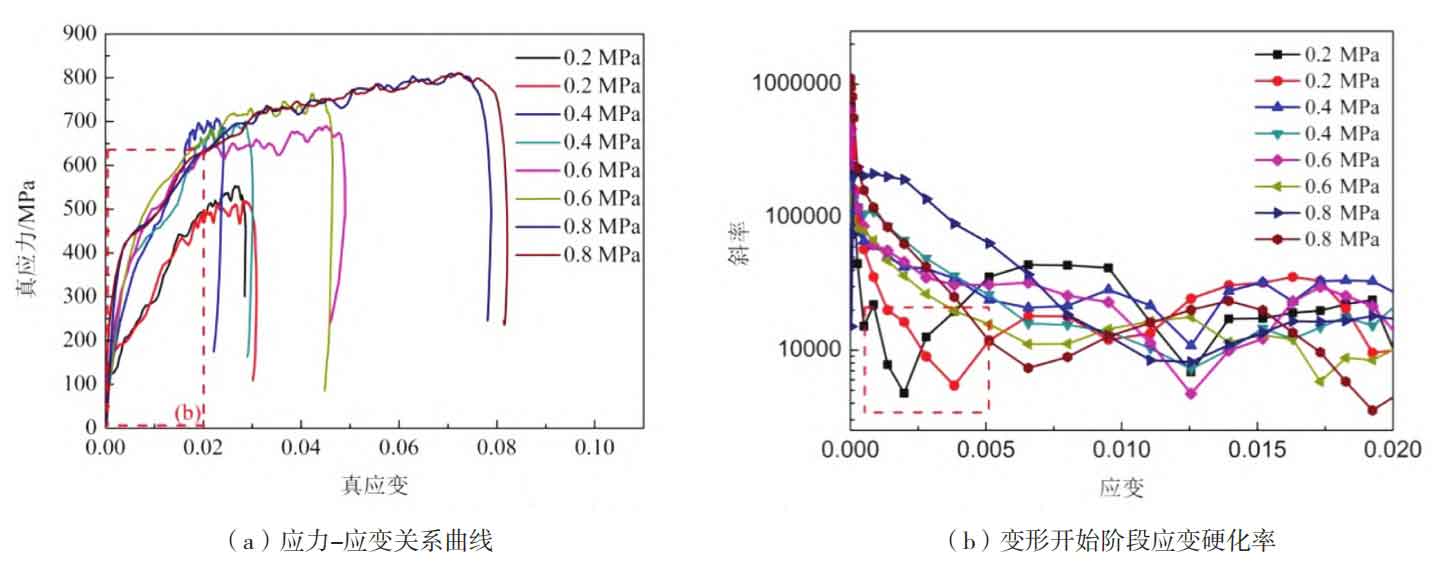
As mentioned earlier, the critical stress values required for the transformation from linear hardening to nonlinear hardening during the deformation process of Mn13Cr2Mo high manganese cast steel under different impact dynamic loads are different, especially when the pressure increases from 0.4 MPa to 0.6 MPa, the critical strength of the transformation significantly increases from 123 MPa to 356 MPa, indicating that the linear strengthening effect of the alloy reaches the optimal state at this time. Analyzing the SHPB test conditions, this phenomenon may be caused by material strain rate hardening. Research has shown that as the impact load increases, the viscous resistance of dislocations induces the occurrence of strain rate hardening mechanism, thereby increasing the critical stress for high manganese cast steel to transition from linear hardening stage to nonlinear hardening stage. As the strain increases, the material deforms and enters the nonlinear hardening zone. At this time, the strain hardening law of Mn13Cr2Mo varies under different impact loads. In order to further clarify the strain hardening rate of the test cast steel in the nonlinear hardening zone under different dynamic loads, Figure 3b shows the variation law of the slope of the stress-strain curve at this stage. As shown in the figure, under the pressure of 0.2 MPa, the deformation hardening rate of the test cast steel is significantly lower than that of the test cast steel under higher pressure (0.4-0.8 MPa), indicating that the hardening rate of the test cast steel in the non-uniform hardening stage is relatively low under 0.2 MPa air pressure, as shown in the icon in box 5b. When the pressure is increased to above 0.4 MPa, the hardening rate of the nonlinear hardening stage of the material under different pressures is similar and maintains a similar variation pattern. By analyzing the variation patterns between different pressures and hardening behaviors during the nonlinear hardening stage, it can be concluded that the differences in hardening behaviors exhibited during the material deformation process may be related to the dislocation growth process. The deformation strengthening law can be understood from the perspective of deformation mechanism as the macroscopic appearance caused by the obstruction of various dislocation slip processes, which is the result of the interaction between dislocation appreciation and dislocation slip. When the pressure is 0.2 MPa, the rate of dislocation growth inside the alloy is relatively slow. Once deformation enters the nonlinear hardening zone, the movement resistance of movable dislocations is relatively small, and the rate of dislocation growth is slow. Dislocations can slip under relatively small stress states, resulting in a lower strain hardening rate; Similarly, when the pressure increases to above 0.4 MPa, due to the dislocation increment excited during the linear deformation stage, including the accumulated larger stress during the linear deformation stage, the dislocation increment during the nonlinear hardening stage is faster. At the same time, the alloy undergoes plastic deformation through multiple slip modes, and the increment of dislocations can act as resistance to the movement of movable dislocations, thereby exhibiting a significant deformation hardening effect in the alloy material during this stage. Figure 4 shows the substructure photos of experimental cast steel under different impact loads obtained by transmission electron microscopy. The characterization results of the substructure indicate that when the impact load is 0.2 MPa, the dislocation density in the matrix is low, and it can be seen that dislocations are distributed in rows on the ferrite matrix, as shown in Figure 4a. As the impact load increased from 0.2 MPa to 0.4 MPa, there was little change in the distribution characteristics of dislocations. Rows of dislocations could still be observed in the matrix, indicating that the dislocation density remained low at this time, as shown in Figure 4b. When the impact load further increased to 0.6 MPa and 0.8 MPa, the dislocation density in the substructure of the test cast steel significantly increased, and even formed a cellular substructure composed of dislocation entanglement structures, as shown in Figures 4c and d. Furthermore, it is worth noting that when the impact load is 0.2 MPa, twinning structures can be observed locally in the substructure. However, when the impact load increases to 0.6 MPa and 0.8 MPa, twinning structures are not observed in the substructure, indicating that as the impact load increases, twinning mechanisms do not play a dominant role in the alloy deformation process. The above experimental results further demonstrate the mechanism of dislocation propagation during the deformation hardening process of Mn13Cr2Mo high manganese cast steel under dynamic load.

In summary, considering the transition stress from linear hardening stage to nonlinear hardening stage and the work hardening rate of the alloy, for the typical Mn13Cr2Mo high manganese wear-resistant cast steel used in the experiment, when the cylinder pressure is higher than 0.6 MPa, the critical stress for the transition from linear hardening stage to nonlinear hardening stage during the deformation process of the test cast steel reaches about 356 MPa. At this time, the strain hardening rate in the nonlinear hardening stage of the material also maintains a high level, This indicates that the experimental Mn13Cr2Mo high manganese cast steel under this stress state has good deformation hardening ability. Based on the application background of this type of alloy mentioned above, it can be seen that this type of alloy is suitable for actual working conditions corresponding to service stress states above 0.6 MPa. Under these conditions, the deformation hardening potential of the high manganese wear-resistant cast steel can be fully utilized, ensuring that the wear-resistant cast steel has excellent wear resistance and service life.
3. Conclusion
(1) The deformation process of Mn13Cr2Mo high manganese cast steel under dynamic load includes two stages: linear hardening and nonlinear hardening, and the strain hardening rate in the nonlinear hardening stage is lower than that in the linear hardening stage.
(2) When the cylinder pressure increases from 0.2 MPa to 0.4 MPa, 0.6 MPa, and 0.8 MPa under dynamic load, the critical transition stresses for linear hardening and nonlinear hardening of Mn13Cr2Mo high manganese cast steel used in the experiment are about 107 MPa, 123 MPa, 356 MPa, and 329 MPa, respectively.
(3) For the experimental Mn13Cr2Mo high manganese cast steel, when the cylinder pressure is greater than 0.6 MPa, the critical transformation stress and strain hardening rate in the nonlinear hardening stage of the material reach the optimal state, and the work hardening ability of the material is significantly enhanced. Under this stress state, the strengthening potential of the alloy is fully stimulated.
