During the filling process of lost foam casting, the flow of liquid metal must meet the hydrodynamic laws, which can be calculated by the complete Navier-Stokes flow equation. First, we need to satisfy the mass conservation continuity equation, which is:
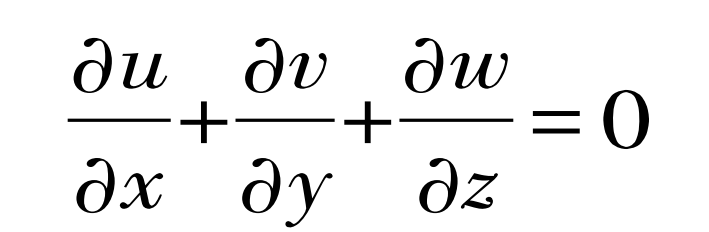
Where: u, v, w are the components of the velocity vector in the x, y, and z directions in the coordinate system.
Assuming that the fluid is incompressible and its density is constant, the simplified momentum equation expression is:
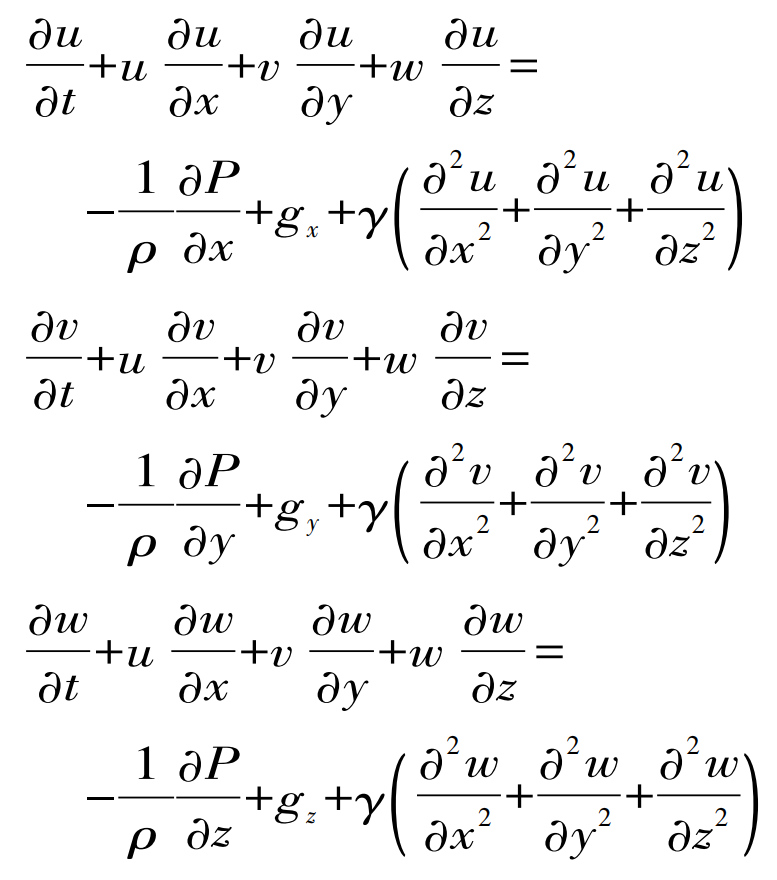
Where: t is time; P is the pressure; Gx, gy and gz are the gravity acceleration components in the three directions of x, y and z in turn; γ Is the kinematic viscosity; ρ Fluid density.
The energy equation is used to describe the temperature change during the filling process of molten metal in lost foam casting, which is:
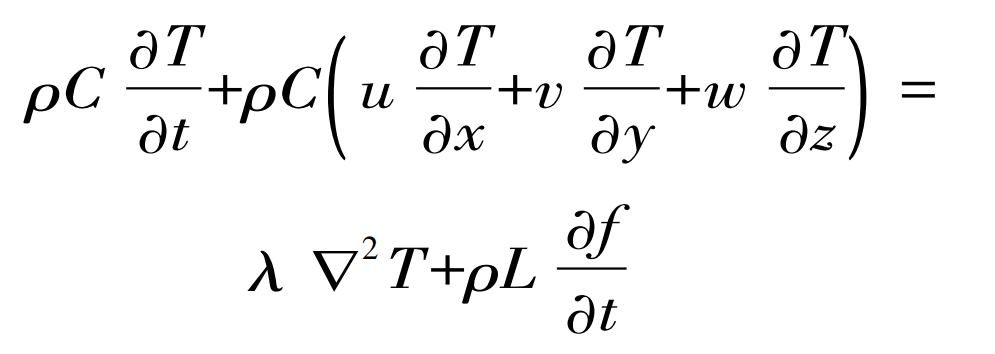
Where: C is the specific heat capacity of the material; T is temperature; λ Is the thermal conductivity; L is the latent heat of solidification; F is the solid fraction; ▽ 2 is the Laplace operator.
During the filling process, there are complex thermodynamic and dynamic changes between the front of the molten metal and the pattern. The pattern is heated, combusted and gasified under the thermal radiation of the high temperature molten metal. There is a gap between the front of the molten metal and the pattern called the air gap layer. Professor Wei Zunjie and other professors put forward the air gap pressure model in the filling process, which is:

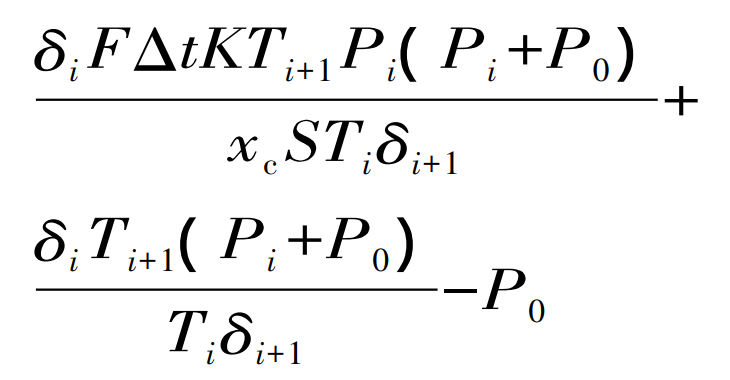
Air gap size Δδ Is:
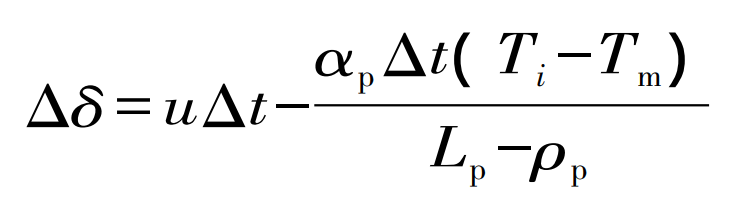
Where, Pi and Pi+1 are the air gap pressure at i and i+1 respectively; δ i、 δ I+1 is the air gap thickness at i and i+1 respectively; P0 is atmospheric pressure; Ti and Ti+1 are the liquid metal temperature at i and i+1 respectively; LP is the gasification latent heat of the pattern; Tm is the temperature of the pattern; Vp is gas generation; K is air permeability; Xc is the thickness; S is the sectional area of the lost foam casting; F is the perimeter of the lost foam casting; Δ T is the time step; α P is the effective convective heat transfer coefficient between the molten metal and the pattern; ρ P is the density of the pattern.
In the mold filling of lost foam casting, if the internal heat conduction of the pattern is not considered, the free surface heat transfer boundary conditions are:
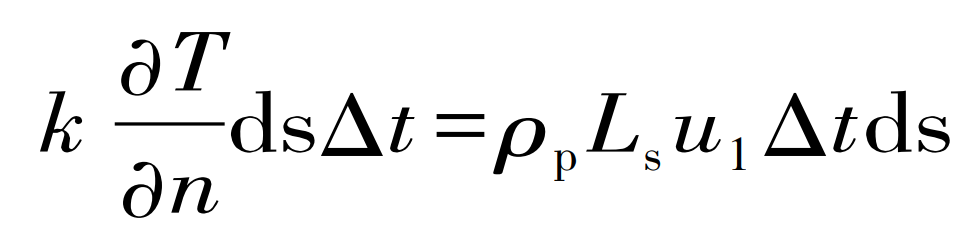
Where, partial T/partial n is the temperature gradient of the liquid metal along the normal direction of the free surface; Ls is the latent heat of the pattern; U1 is the flow velocity of liquid metal along the normal direction of the free surface; K is the heat transfer coefficient; Ds is the free surface area of a calculation unit.
