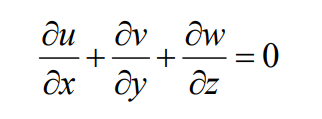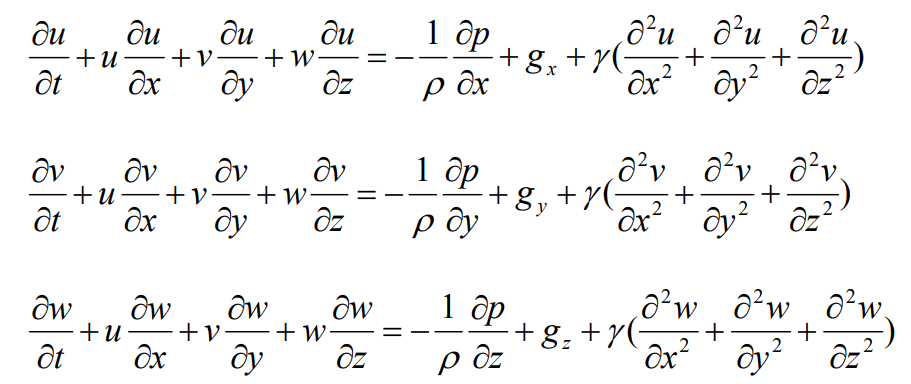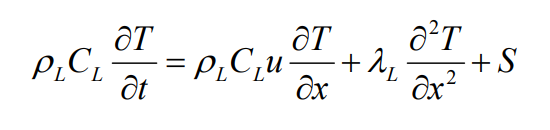Whether the selection of mathematical model is reasonable or not directly imagines the accuracy of the whole simulation process, which plays a very important role in simulation calculation.
In the filling process of lost foam casting, although the front metal liquid at the flow front is hindered by the air gap pressure generated by pattern decomposition, it is still a viscous and incompressible Newtonian fluid in essence. Therefore, its flow follows the law of fluid dynamics, and its motion state can be described by the basic control equations of mass conservation and momentum conservation. The heat exchange between liquid metal and mold in the filling process of lost foam casting can be described by heat balance equation.
For the passive flow field of incompressible fluid, at any point in the flow domain filled with fluid, the divergence of fluid velocity should be equal to 0, that is, mass conservation. Its mathematical form is:
Law of conservation of mass continuity equation:
Law of conservation of momentum – Navier Stokes equation:
In the above formula, u, V and W are instantaneous velocity components (M / s) in X, y and Z coordinate directions respectively;
P is the instantaneous pressure on the unit (PA);
GX, y g and Z G are the components of gravitational acceleration in the three coordinate directions of X, y and Z respectively (M / S2);
ρ 、 γ They are the density (kg / M) and kinematic viscosity (m2 / s) of the fluid respectively.
During the filling process of lost foam casting, the foam pattern is decomposed and decomposed under the action of high temperature molten metal at the filling front of lost foam casting. This is an endothermic process, so the temperature of molten metal at the filling front of lost foam casting will decrease. When choosing the mathematical model, the heat exchange between the front liquid metal and the pattern must be taken into account.
Therefore, in addition to the basic governing equations of the law of conservation of mass and the law of conservation of momentum, it is also necessary to solve the energy equation:
In the formula, the mathematical analytical solutions of partial differential equations are difficult to obtain accurately, so only the numerical solution method can be used to obtain their mathematical analytical solutions. The essence of numerical solution is to discretize the continuous solution space into finite relatively independent micro elements, and then solve these independent micro elements separately. Finally, all the solution results are continuous in time as the result of the whole solution goal.